A rather widespread rumour tells of how the owners of a famous car, produced by a well known Italian car manufacturer in the 1980s, which was very often white in colour, often opened by mistake someone else’s car with their own key, when confusing it with their own car in a parking lot, maybe when leaving the cinema or a concert.
Maybe it is just an urban myth, but it does make one reflect on an important security issue: how many different keys exist for a given lock? In other words, what is the probability that a person in possession of a key can open another lock of the same type, as well as their own? This is not just a mere curiosity. There are situations in which this can actually happen. For example, there are dozens of mailboxes with the same lock in a large condominium: is it possible that a key can open more than one?Let’s make some calculations. The number of keys theoretically possible for a padlock, cylinder lock or pin type lock depends on the number of possible bittings for that particular lock, that is, the number of possible combinations between the heights of the pins inserted into the plug; the combinations are calculated by taking the number of possible heights of the pins and raising them to the power of the number of pins themselves.
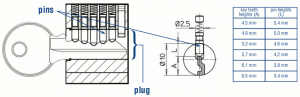 For this reason, more precise machining can achieve more secure locks, as it allows a greater number of pins to be inserted in a given plug and to obtain from the same piston – with equal length – a greater number of heights. This translates into a significant increase in the number of possible combinations. For example: a lock with 3 pins with 4 heights each might only have 43= 64 theoretical combinations. If, by means of more precise machining, one achieves 5 heights rather than 4, the combinations become 53=125. If one then manages to insert 4 pins instead of 3, there are 625 combinations (54 ), and so on.
For this reason, more precise machining can achieve more secure locks, as it allows a greater number of pins to be inserted in a given plug and to obtain from the same piston – with equal length – a greater number of heights. This translates into a significant increase in the number of possible combinations. For example: a lock with 3 pins with 4 heights each might only have 43= 64 theoretical combinations. If, by means of more precise machining, one achieves 5 heights rather than 4, the combinations become 53=125. If one then manages to insert 4 pins instead of 3, there are 625 combinations (54 ), and so on.
It is then necessary to take into account that one must eliminate some of the bittings theoretically possible . Initially, it is necessary to eliminate all those in which all the pins have the same height. These are obviously not secure, since the lock could be opened by using any disc or metal tool which simultaneously lowers all the pins. Secondly, one must eliminate those which have too abrupt an alternation between maximum and minimum heights of the pins and which, therefore, can make it difficult to insert and/or extract the key. These combinations are hardly ever eliminated in poor quality locks, whilst the importance of eliminating them makes it even more vital to have a large number of theoretically possible bittings, given that the number effectively usable is actually less. Looking at the most simplest example, that of the lock with 3 pins and 4 heights, there are 4 combinations with the pins at the same height, which, having removed them, leaves 60 possible combinations, and 14 combinations where a maximum height and a minimum height are consecutive, which, after they are removed, only leaves 46 combinations which are actually usable. If a lock of this type is used for the mail boxes in a condominium with more than 46 apartments it is statistically certain that there is at least one occupant who can read someone else’s mail…
Has it ever happened that you have opened another lock with your key?
Look how a lock is assembled
You can see the catalogue of Viro products here

I once bought a Toyota sr5 brand new and two years later bought a Toyota pickup truck.I was amazed when I accidentally discovered both sets of keys worked on each vehicle
very clear and good article easy to understand. Thank you